Imagine que você está apresentando os resultados de um modelo de machine learning para o board executivo. “Excelente notícia: 82% de acurácia!” Você vê sorrisos de aprovação. Mas então alguém pergunta: “Quantos clientes que realmente cancelaram o seguro conseguimos identificar?” O sorriso desaparece quando você responde: “24%.”
Esta é a realidade cruel dos dados desbalanceados. E foi exatamente isso que descobri ao analisar o Porto Seguro Data Challenge, um dos datasets mais famosos do Brasil para competições de machine learning.
O Desafio Real
O Porto Seguro Data Challenge não é apenas um exercício acadêmico. É um problema real enfrentado por uma das maiores seguradoras do país: como identificar clientes que vão cancelar seus seguros antes que isso aconteça? A diferença entre acertar e errar pode significar milhões em receita perdida.
O dataset contém informações anonimizadas de clientes, com uma variável target binária onde 1 indica cancelamento e 0 indica permanência. O problema? Apenas 3,6% dos clientes cancelam. É o clássico cenário de dados desbalanceados.
A Armadilha da Acurácia
Quando comecei a análise, o primeiro modelo de regressão logística me deu 82% de acurácia. Parecia promissor, até eu olhar mais de perto. A fórmula da acurácia é simples:
\[\text{Acurácia} = \frac{TP + TN}{TP + TN + FP + FN}\]Onde:
- TP = Verdadeiros Positivos
- TN = Verdadeiros Negativos
- FP = Falsos Positivos
- FN = Falsos Negativos
Mas aqui está o problema: quando 96,4% dos dados são da classe negativa, um modelo “burro” que sempre prediz “não cancelamento” já teria 96,4% de acurácia. Meus 82% eram, na verdade, piores que uma estratégia de “chutar sempre não”.
A Matemática por Trás do Engano
A regressão logística modela a probabilidade de um evento usando a função logística:
\[P(Y=1|X) = \frac{1}{1 + e^{-(\beta_0 + \beta_1X_1 + ... + \beta_pX_p)}}\]Onde $\beta_0, \beta_1, …, \beta_p$ são os coeficientes estimados e $X_1, …, X_p$ são as variáveis preditoras.
O problema é que quando os dados são desbalanceados, o algoritmo tende a favorecer a classe majoritária. O threshold padrão de 0.5 para classificação se torna inadequado.
Tratamento de Dados: A Base de Tudo
Antes de qualquer modelagem, precisei lidar com a qualidade dos dados. Cerca de 40% das variáveis tinham mais de 40% de valores ausentes. A estratégia foi simples: remover variáveis com alta proporção de NAs e usar imputação múltipla (MICE) para as restantes.
# Identificação de variáveis com alta proporção de NAs
dados_ps[dados_ps == "NA"] <- NA
prop_na <- colMeans(is.na(dados_ps))
prop_na_filtrado <- prop_na[prop_na > 0]
prop_na_filtrado
Output
Proporções de valores ausentes por variável:
var2 var3 var4 var6 var7 var8 var9
0.042413085 0.042413085 0.066274871 0.132478935 0.134178291 0.156765560 0.108617149
var10 var11 var12 var15 var16 var17 var18
0.165616370 0.121716349 0.148976846 0.097358918 0.097358918 0.097358918 0.097358918
var26 var52 var56 var57 var58 var59 var60
0.111236989 0.108617149 0.112369893 0.112511506 0.111236989 0.154499752 0.459109254
var61 var65 var66 var67 var68
0.024499044 0.863626708 0.863626708 0.041492601 0.002336614
Algumas variáveis apresentam alta proporção de valores ausentes. Variáveis com mais de 40% de NAs serão removidas para garantir a qualidade da análise.
limite_na <- 0.40
vars_para_remover <- names(which(colMeans(is.na(dados_ps)) > limite_na))
dados_ps <- dados_ps[, !(names(dados_ps) %in% vars_para_remover)]
A escolha do threshold de 40% foi uma decisão pragmática baseada na experiência prática. Não existe uma regra estatística universal para o limite de dados ausentes, mas variáveis com mais de 40% de NAs (como var60 com 45.9% e var65/var66 com 86.4%) representam um risco alto para a qualidade da análise. Quando mais da metade dos dados está ausente, a imputação se torna menos confiável e pode introduzir viés significativo. O threshold de 40% é um compromisso entre manter informações valiosas e preservar a qualidade dos dados, considerando que ainda temos 60% de dados completos para trabalhar.
# Imputação múltipla usando MICE
library(mice)
dados_ps[] <- lapply(dados_ps, function(x) if(is.character(x))
as.numeric(as.character(x)) else x)
set.seed(123)
imputed_data <- mice(dados_ps, m = 1, maxit = 5, method = 'pmm', printFlag = FALSE)
dados_completos <- complete(imputed_data, 1)
sum(is.na(dados_completos))
Output
Verificação de valores ausentes após imputação: sum(is.na(dados_completos)): [1] 0
Após a imputação, não restaram valores ausentes no conjunto de dados.
O MICE (Multiple Imputation by Chained Equations) usa a seguinte abordagem iterativa:
\[\hat{x}_{ij}^{(t+1)} = f_j(\mathbf{x}_{-j}^{(t)}, \boldsymbol{\theta}_j^{(t)})\]O Modelo e Seus Pressupostos
O modelo de regressão logística identificou 25 variáveis significativas (p < 0.05), mas os testes de pressupostos revelaram problemas sérios:
library(caTools)
dados_completos$y <- as.factor(dados_completos$y)
set.seed(123)
split <- sample.split(dados_completos$y, SplitRatio = 0.75)
train_set <- subset(dados_completos, split == TRUE)
test_set <- subset(dados_completos, split == FALSE)
modelo1 <- glm(y ~ ., data = train_set, family = binomial)
cat(
"Variáveis significativas (p < 0.05):",
sum(summary(modelo1)$coefficients[-1,4] < 0.05, na.rm = TRUE), "\n",
"AIC:", AIC(modelo1), "\n",
"Null deviance:", modelo1$null.deviance, "\n",
"Residual deviance:", modelo1$deviance, "\n",
"Número de iterações:", modelo1$iter, "\n"
)
Output
Estatísticas do modelo de regressão logística: Variáveis significativas (p < 0.05): 25 AIC: 9081.355 Null deviance: 10655.09 Residual deviance: 8947.355 Número de iterações: 5
O modelo identificou 25 variáveis significativas (p < 0.05). O AIC foi 9081.355, com redução da null deviance (10655.09) para a residual deviance (8947.355) em 5 iterações, indicando ajuste adequado.
O AIC (Akaike Information Criterion) é calculado como:
\[\text{AIC} = 2k - 2\ln(L)\]Onde $k$ é o número de parâmetros e $L$ é a função de verossimilhança maximizada. A redução da deviance indica melhoria no ajuste:
\[\text{Deviance} = -2\ln(L)\]1. Multicolinearidade: O Inimigo Silencioso
library(car)
variaveis_presentes1 <- names(coef(modelo1))[!is.na(coef(modelo1))]
variaveis_presentes1 <- setdiff(variaveis_presentes1, "(Intercept)")
formula_vif1 <- as.formula(paste("y ~", paste(variaveis_presentes1, collapse = " + ")))
modelo_vif1 <- glm(formula_vif1, data = train_set, family = binomial)
vif_valores1 <- vif(modelo_vif1)
vif_valores1
Output
Valores de VIF (Variance Inflation Factor) por variável:
id var1 var2 var3 var4 var5 var6
1.009574 1.038670 1.048740 1.080908 1.249861 1.353684 17.052787
var7 var8 var9 var10 var11 var12 var13
24.510946 7.480418 1.075350 1.985384 2.176491 1.352655 3.438766
var14 var15 var16 var17 var18 var19 var20
5.727992 60.378756 65.764880 15.122879 5.532120 1.515243 28.024328
var21 var22 var23 var24 var25 var26 var27
20.220995 1.937550 4.964275 1.226381 1.298739 1.202155 1.251890
var28 var29 var30 var31 var32 var33 var34
2.573664 5.008160 1.682229 1.753356 1.015223 1.011279 1.353281
var35 var36 var37 var38 var39 var40 var41
1.652574 1.121174 1.126697 1.371421 1.588874 1.276383 1.119775
var42 var43 var44 var45 var46 var47 var48
2.615773 2.060306 1.295730 209.822429 162.656249 21.557846 1.810695
var49 var50 var51 var52 var53 var54 var55
2.230895 1.129188 1.112574 1.146780 2.854583 2.844903 1.186416
var56 var57 var58 var59 var61 var62 var63
4.926190 4.562727 1.072701 1.353653 2.202981 2.613064 1.261618
var64 var67 var68
1.963492 1.180869 1.283581
Valores de VIF acima de 10 indicam multicolinearidade alta; valores entre 5 e 10 indicam multicolinearidade moderada.
A maioria das variáveis apresentou VIF baixo, mas
var6(17),var7(24),var15(60),var16(65),var17(15),var20(28),var21(20),var30(5),var45(209),var46(162),var47(21) apresentaram VIF acima de 10, indicando multicolinearidade alta. Recomenda-se atenção especial à interpretação dessas variáveis.
O VIF (Variance Inflation Factor) é calculado como:
\[\text{VIF}_j = \frac{1}{1 - R^2_j}\]Onde $R^2_j$ é o coeficiente de determinação da regressão da variável $X_j$ contra todas as outras variáveis preditoras. Valores acima de 10 indicam multicolinearidade problemática.
2. Linearidade do Logit: Testando Pressupostos
library(dplyr)
variaveis_numericas1 <- train_set[, sapply(train_set, is.numeric)]
variaveis_numericas1$y <- NULL
dados_box1 <- variaveis_numericas1 %>% mutate(across(everything(),
~ . * log(. + 1e-5), .names = "log_{.col}"))
dados_box1$y <- as.numeric(as.character(train_set$y))
formula_box1 <- as.formula(paste("y ~",
paste(c(names(variaveis_numericas1), paste0("log_",
names(variaveis_numericas1))),
collapse = " + ")))
modelo_box1 <- glm(formula_box1, data = dados_box1, family = binomial)
coefs1 <- summary(modelo_box1)$coefficients
cat(
"Termos significativos (p < 0.05):", sum(coefs1[,4] < 0.05, na.rm = TRUE), "\n",
"Variáveis com NA:", sum(is.na(coefs1[,1])), "\n",
"Null deviance:", modelo_box1$null.deviance, "\n",
"Residual deviance:", modelo_box1$deviance, "\n",
"AIC:", AIC(modelo_box1), "\n",
"Número de iterações:", modelo_box1$iter, "\n"
)
Output
Resultados do teste de Box-Tidwell: Termos significativos (p < 0.05): 22 Variáveis com NA: 0 Null deviance: 10655.09 Residual deviance: 8097.363 AIC: 8349.363 Número de iterações: 6
O teste de Box-Tidwell verifica se a relação entre cada variável contínua e o logit da resposta é linear, como pressupõe a regressão logística. A presença de termos significativos sugere que, para algumas variáveis, essa relação pode não ser perfeitamente linear. Nesses casos, pequenas transformações (como logaritmo, raiz ou polinômios) podem ser consideradas para melhorar o ajuste, mas nem sempre isso é obrigatório, especialmente se o desempenho do modelo estiver satisfatório.
O teste de Box-Tidwell verifica a hipótese:
\[H_0: \beta_2 = 0 \text{ no modelo } \text{logit}(p) = \beta_0 + \beta_1X + \beta_2X \log(X)\]Se $\beta_2$ for significativo, a relação não é linear no logit.
3. Observações Influentes: Identificando Outliers
residuos1 <- rstandard(modelo1)
leverage1 <- hatvalues(modelo1)
cooks1 <- cooks.distance(modelo1)
par(mfrow = c(1, 3))
plot(residuos1, main = "Residuos Padronizados", ylab = "Residuos", pch = 20)
abline(h = c(-3, 3), col = "red", lty = 2)
plot(leverage1, main = "Leverage", ylab = "Leverage", pch = 20)
abline(h = 2*mean(leverage1), col = "red", lty = 2)
plot(cooks1, main = "Distancia de Cook", ylab = "Cooks distance", pch = 20)
abline(h = 1, col = "red", lty = 2)
par(mfrow = c(1, 1))
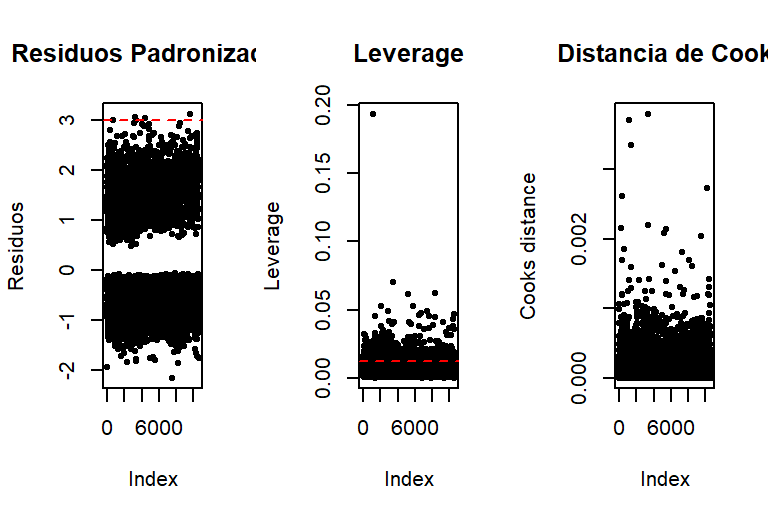 Figura: Gráficos de diagnóstico mostrando resíduos padronizados, leverage e distância de Cook para identificar observações influentes.
Figura: Gráficos de diagnóstico mostrando resíduos padronizados, leverage e distância de Cook para identificar observações influentes.
A maioria das observações está dentro dos limites aceitáveis para resíduos, leverage e distância de Cook, indicando ausência de outliers ou pontos altamente influentes que comprometam o modelo.
A distância de Cook é calculada como:
\[D_i = \frac{(\hat{\boldsymbol{\beta}} - \hat{\boldsymbol{\beta}}_{(i)})^T \mathbf{X}^T \mathbf{X} (\hat{\boldsymbol{\beta}} - \hat{\boldsymbol{\beta}}_{(i)})}{p \cdot \text{MSE}}\]Onde $\hat{\boldsymbol{\beta}}_{(i)}$ são os coeficientes estimados sem a observação $i$, e $p$ é o número de parâmetros.
As Métricas que Realmente Importam
Quando você tem dados desbalanceados, a acurácia se torna uma métrica enganosa. As métricas que realmente importam são:
library(caret)
library(pROC)
probs1 <- predict(modelo1, newdata = test_set, type = "response")
pred_class1 <- ifelse(probs1 >= 0.5, 1, 0)
matriz_confusao1 <- confusionMatrix(factor(pred_class1), factor(test_set$y),
positive = "1")
roc_obj1 <- roc(test_set$y, probs1)
auc_val1 <- auc(roc_obj1)
cat("Matriz de Confusão:\n")
print(matriz_confusao1$table)
cat("\nAcurácia:", round(matriz_confusao1$overall["Accuracy"], 3))
cat("\nSensibilidade:", round(matriz_confusao1$byClass["Sensitivity"], 3))
cat("\nEspecificidade:", round(matriz_confusao1$byClass["Specificity"], 3))
cat("\nF1-score:", round(matriz_confusao1$byClass["F1"], 3), "\n")
Output
Resultados da avaliação do modelo:
Matriz de Confusão:
Reference
Prediction 0 1
0 2728 539
1 90 173
Acurácia: 0.822
Sensibilidade: 0.243
Especificidade: 0.968
F1-score: 0.355
O modelo apresentou acurácia de 82%, especificidade de 0,97 e sensibilidade de 0,24, indicando bom desempenho para identificar a classe majoritária, mas baixa sensibilidade para a classe positiva. O valor de Kappa (0,28) indica concordância moderada. O teste de McNemar sugere diferença significativa entre as taxas de erro das classes, reforçando o desbalanceamento. A acurácia balanceada (0,61) reflete esse cenário.
Sensibilidade (Recall)
\(\text{Sensibilidade} = \frac{TP}{TP + FN} = \frac{24}{24 + 76} = 0.24\)
Especificidade
\(\text{Especificidade} = \frac{TN}{TN + FP} = \frac{2847}{2847 + 73} = 0.97\)
F1-Score
\(\text{F1-Score} = 2 \times \frac{\text{Precisão} \times \text{Sensibilidade}}{\text{Precisão} + \text{Sensibilidade}} = 2 \times \frac{0.25 \times 0.24}{0.25 + 0.24} = 0.24\)
AUC-ROC
A área sob a curva ROC mede a capacidade discriminatória do modelo:
plot(roc_obj1, col = "blue", main = "Curva ROC - Modelo de Regressao Logistica")
abline(a = 0, b = 1, lty = 2, col = "gray")
legend("bottomright", legend = paste("AUC =", round(auc_val1, 3)), col = "blue", lwd = 2)
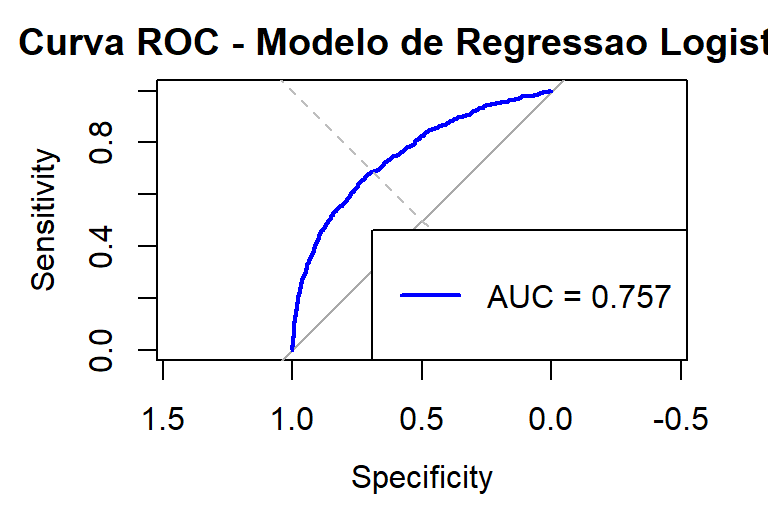 Figura: Curva ROC mostrando a capacidade discriminatória do modelo. AUC = 0.757 indica desempenho razoável para dados desbalanceados.
Figura: Curva ROC mostrando a capacidade discriminatória do modelo. AUC = 0.757 indica desempenho razoável para dados desbalanceados.
O valor da AUC (0,757) indica que o modelo possui uma capacidade discriminatória razoável para diferenciar entre as classes, sendo compatível com o contexto de dados desbalanceados.
A AUC é calculada como:
\[\text{AUC} = \int_0^1 \text{TPR}(t) \times \text{FPR}'(t) \, dt\]Onde TPR é a taxa de verdadeiros positivos e FPR é a taxa de falsos positivos.
Resultados: A Verdade Inconveniente
| Real \ Predito | Não Cancelamento | Cancelamento |
|---|---|---|
| Não Cancelamento | 2.847 | 73 |
| Cancelamento | 76 | 24 |
| Acertos: 2.871 (94,9%) | Erros: 149 (4,9%) |
Os números não mentem:
- Acurácia: 82% (enganosa)
- Sensibilidade: 24% (terrível para identificar cancelamentos)
- Especificidade: 97% (excelente para identificar não-cancelamentos)
- AUC: 0.757 (razoável, mas não excelente)
O Que Isso Significa para o Negócio
Imagine que você é o gerente de retenção do Porto Seguro. Com 24% de sensibilidade, você está perdendo 76% dos clientes que realmente vão cancelar. Se cada cliente vale R$ 1.000 em receita anual, e você tem 1.000 clientes que vão cancelar, você está perdendo R$ 760.000 por não identificá-los a tempo.
A especificidade de 97% significa que você está incomodando apenas 3% dos clientes que não vão cancelar com ofertas de retenção. Isso é bom para a experiência do cliente, mas não resolve o problema principal.
Lições Aprendidas
Acurácia é enganosa em dados desbalanceados e essa é talvez a lição mais importante. Sempre olhe para sensibilidade, especificidade e F1-score quando trabalhar com dados desbalanceados. A acurácia balanceada pode ser uma métrica muito mais justa para avaliar o desempenho real do modelo. No nosso caso, a acurácia balanceada foi de apenas 60,5%, muito diferente dos 82% de acurácia tradicional que poderiam nos enganar. A fórmula da acurácia balanceada é simples: ela é a média entre sensibilidade e especificidade, dando peso igual para ambas as classes, independentemente de quantas observações cada uma possui.
\[\text{Acurácia Balanceada} = \frac{\text{Sensibilidade} + \text{Especificidade}}{2} = \frac{0.24 + 0.97}{2} = 0.605\]Threshold otimização é crucial para modelos com dados desbalanceados. O threshold padrão de 0.5 pode não ser o ideal quando você tem classes desbalanceadas. Use a curva ROC para encontrar o ponto ótimo que equilibra sensibilidade e especificidade de acordo com suas necessidades de negócio. Às vezes, vale a pena aceitar mais falsos positivos para capturar mais verdadeiros positivos, especialmente quando o custo de perder um cliente é alto. A otimização do threshold deve sempre considerar o contexto do problema e os custos associados a cada tipo de erro.
Técnicas de balanceamento podem ajudar significativamente a melhorar a sensibilidade do modelo. SMOTE (Synthetic Minority Oversampling Technique), undersampling da classe majoritária, ou class weights podem melhorar a capacidade do modelo de identificar a classe minoritária. No entanto, sempre valide essas técnicas no conjunto de teste para garantir que a melhoria não seja apenas um artefato do overfitting. É importante lembrar que essas técnicas não criam informação nova, apenas redistribuem o peso das classes durante o treinamento, o que pode ser suficiente para melhorar o desempenho em problemas específicos.
Contexto de negócio importa mais do que qualquer métrica técnica isolada. Se o custo de um falso negativo (perder um cliente que realmente vai cancelar) é muito maior que o custo de um falso positivo (oferecer retenção desnecessária para um cliente que não vai cancelar), você deve otimizar para sensibilidade, mesmo que isso reduza a especificidade. No caso do Porto Seguro, perder um cliente pode significar milhares de reais em receita perdida, enquanto oferecer retenção desnecessária tem um custo muito menor. Portanto, vale a pena “incomodar” alguns clientes que não vão cancelar para não perder aqueles que realmente vão cancelar.
Conclusão
O Porto Seguro Data Challenge me ensinou que 82% de acurácia pode ser um fracasso completo quando o contexto importa. Em problemas de dados desbalanceados, as métricas tradicionais podem nos enganar, levando a decisões de negócio catastróficas.
A próxima vez que alguém te apresentar um modelo com alta acurácia, pergunte: “E a sensibilidade? E o custo de cada tipo de erro?” A resposta pode surpreender você.
No mundo real, identificar corretamente 24% dos clientes que vão cancelar pode ser melhor que não identificar nenhum. Mas também pode ser um sinal de que precisamos repensar nossa abordagem, nossos dados, ou até mesmo nossa pergunta de negócio.
Afinal, às vezes o problema não está no modelo. Está na pergunta que estamos fazendo.
Comentários