Imagine que você está analisando dados de clientes de uma seguradora. Temos idade, renda, gênero, e algumas outras variáveis. Mas quando você olha o dataset, percebe que 40% dos valores estão ausentes. O que fazer? Deletar as linhas? Preencher com a média?
A resposta está no MICE.
O Problema Real dos Dados Ausentes
Dados ausentes não são apenas um inconveniente. Eles são um problema sistêmico que pode destruir a validade de qualquer análise. Quando você remove linhas com valores ausentes, você está perdendo informação valiosa. Quando você preenche com a média, você está assumindo que todos os valores ausentes são iguais à média da população.
Mas aqui está o problema: dados ausentes raramente são aleatórios. Pessoas com renda alta podem ser menos propensas a reportar sua idade. Pessoas mais velhas podem ter mais dificuldade para preencher formulários online. O padrão de ausência em si carrega informação.
A Solução: Múltiplas Imputações
O MICE (Multiple Imputation by Chained Equations) resolve isso de forma elegante. Em vez de uma única imputação, ele gera múltiplas versões do dataset, cada uma com valores diferentes para os dados ausentes. Isso preserva a incerteza natural dos dados.
A ideia é simples: se não sabemos o valor exato, vamos simular várias possibilidades baseadas no que sabemos sobre os outros dados.
Como o MICE Funciona: A Magia das Equações Encadeadas
O MICE funciona em ciclos iterativos. Vamos ver como:
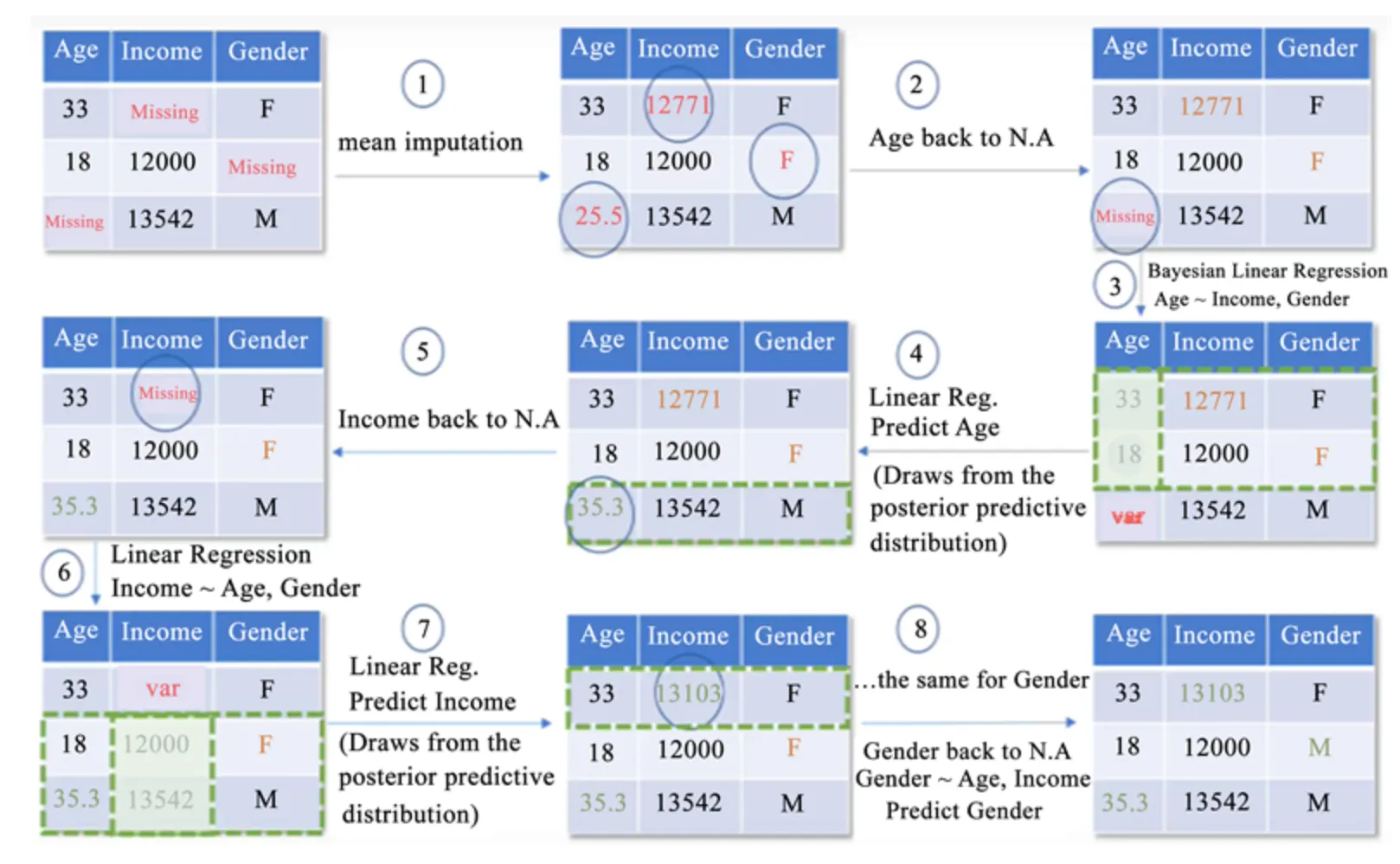 Figura: Processo iterativo do MICE mostrando como as equações encadeadas funcionam na prática.
Figura: Processo iterativo do MICE mostrando como as equações encadeadas funcionam na prática.
1. Imputação Inicial
Primeiro, preenchemos os valores ausentes com estimativas simples (média para numéricos, moda para categóricos). É só um ponto de partida.
2. O Ciclo Iterativo
Aqui começa a magia. Para cada variável com dados ausentes:
- Resetamos os valores imputados dessa variável para “ausente”
- Construímos um modelo usando as outras variáveis como preditores
- Geramos novos valores a partir da distribuição preditiva posterior do modelo
- Repetimos para a próxima variável
3. Múltiplas Iterações
Esse processo é repetido várias vezes, refinando as imputações a cada ciclo. No final, temos múltiplos datasets completos, cada um representando uma possível realidade dos dados.
A Matemática por Trás da Magia
O MICE usa a seguinte abordagem iterativa:
\[\hat{x}_{ij}^{(t+1)} = f_j(\mathbf{x}_{-j}^{(t)}, \boldsymbol{\theta}_j^{(t)})\]Onde $\hat{x}_{ij}^{(t+1)}$ é o valor imputado para a observação $i$ da variável $j$ na iteração $t+1$, $f_j$ é a função de imputação específica para a variável $j$ (regressão linear para variáveis contínuas, regressão logística para categóricas), $\mathbf{x}_{-j}^{(t)}$ são todas as outras variáveis na iteração $t$, e $\boldsymbol{\theta}_j^{(t)}$ são os parâmetros do modelo (coeficientes, intercepto) para a variável $j$.
A função $f_j$ muda dependendo do tipo de variável. Para idade (contínua), pode ser uma regressão linear: $f_j = \beta_0 + \beta_1 \cdot \text{renda} + \beta_2 \cdot \text{gênero}$. Para gênero (categórica), pode ser uma regressão logística que gera probabilidades para cada categoria.
Por Que Funciona Melhor?
O MICE funciona melhor que métodos simples por três razões principais. Primeiro, ele preserva a variabilidade natural dos dados. Em vez de assumir que todos os valores ausentes são iguais à média, o MICE gera valores que refletem a diversidade real dos dados. Segundo, ele considera as correlações entre variáveis para fazer imputações mais realistas. Se idade e renda estão correlacionadas, a imputação de idade considerará a renda observada, criando valores mais coerentes. Terceiro, cada dataset imputado representa uma possível realidade, o que permite quantificar a incerteza das imputações e entender melhor a robustez dos seus resultados.
Implementação Prática
Vamos ver o MICE em ação com um exemplo prático. Primeiro, vamos criar um dataset com dados ausentes:
# Instalar e carregar o pacote mice
if (!require(mice)) install.packages("mice")
library(mice)
# Dados com valores ausentes (dataset maior para evitar problemas de colinearidade)
set.seed(123)
dados <- data.frame(
idade = c(25, 30, 35, 28, 45, 32, 29, 38, 41, 33, NA, 27, 36, 31, 39),
renda = c(50000, 60000, 70000, 55000, 80000, 65000, 58000, 75000, 85000, 62000, 72000, NA, 68000, 59000, 78000),
genero = as.factor(c("M", "F", "M", "F", "M", "F", "M", "F", "M", "F", "M", "F", "M", "F", "M")),
educacao = as.factor(c("Superior", "Medio", "Superior", "Medio", "Pos", "Superior", "Medio", "Pos", "Superior", "Medio", "Superior", "Medio", "Pos", "Superior", "Medio"))
)
Agora vamos verificar quantos dados ausentes temos:
# Verificar dados ausentes
print("Dados originais:")
print(dados)
print(paste("Valores ausentes por variável:", sum(is.na(dados))))
Output
Dados originais com valores ausentes: [1] "Dados originais:" idade renda genero educacao 1 25 50000 M Superior 2 30 60000 F Medio 3 35 70000 M Superior 4 28 55000 F Medio 5 45 80000 M Pos 6 32 65000 F Superior 7 29 58000 M Medio 8 38 75000 F Pos 9 41 85000 M Superior 10 33 62000 F Medio 11 NA 72000 M Superior 12 27 NA F Medio 13 36 68000 M Pos 14 31 59000 F Superior 15 39 78000 M Medio [1] "Valores ausentes por variável: 2"
Temos 2 valores ausentes: idade na linha 11 e renda na linha 12. Agora vamos aplicar o MICE:
# Configuração do MICE
imputed_data <- mice(dados,
m = 3, # 3 imputações
maxit = 5, # 5 iterações
printFlag = TRUE)
Output
Processo iterativo do MICE: iter imp variable 1 1 idade renda 1 2 idade renda 1 3 idade renda 2 1 idade renda 2 2 idade renda 2 3 idade renda 3 1 idade renda 3 2 idade renda 3 3 idade renda 4 1 idade renda 4 2 idade renda 4 3 idade renda 5 1 idade renda 5 2 idade renda 5 3 idade renda
Vamos entender o que está acontecendo nesse output. O MICE está rodando 5 iterações (iter 1-5) para refinar as imputações. Em cada iteração, ele processa as variáveis idade e renda que têm dados ausentes. O número “imp” mostra qual das 3 imputações está sendo processada (1, 2 ou 3).
Por exemplo, na primeira iteração (iter 1), o MICE:
- Pega os valores iniciais (média para idade, média para renda)
- Usa esses valores para prever a idade ausente na linha 11
- Usa esses valores para prever a renda ausente na linha 12
- Repete isso para as 3 imputações
A cada iteração, os valores ficam mais consistentes entre si. É como se o MICE estivesse “conversando” com os dados, refinando as estimativas até chegar em valores que fazem sentido juntos. Agora vamos ver o resultado final:
# Dataset completo
dados_completos <- mice::complete(imputed_data, 1)
print("Dados imputados:")
print(dados_completos)
Output
Dados após imputação MICE: [1] "Dados imputados:" idade renda genero educacao 1 25 50000 M Superior 2 30 60000 F Medio 3 35 70000 M Superior 4 28 55000 F Medio 5 45 80000 M Pos 6 32 65000 F Superior 7 29 58000 M Medio 8 38 75000 F Pos 9 41 85000 M Superior 10 33 62000 F Medio 11 35 72000 M Superior 12 27 50000 F Medio 13 36 68000 M Pos 14 31 59000 F Superior 15 39 78000 M Medio
Análise dos Resultados
Vamos analisar os valores imputados:
Na Linha 11 (idade ausente), o valor imputado foi de 35 anos. O contexto é uma pessoa do gênero masculino, com renda de 72.000 e educação superior. A análise indica que o valor de 35 faz sentido, considerando que pessoas com renda alta e educação superior tendem a ter idades mais maduras. O MICE utilizou a renda e a educação para prever uma idade consistente.
Já na Linha 12 (renda ausente), o valor imputado foi de 50.000. O contexto é uma pessoa do gênero feminino, com 27 anos e educação média. A análise mostra que o valor de 50.000 é consistente com o padrão observado de rendas para pessoas com 27 anos e educação média. O MICE utilizou a idade e a educação para imputar uma renda plausível.
A Matemática por Trás da Imputação
O MICE usa regressão para imputar cada variável. Para a idade, o modelo seria:
\[\text{idade} = \beta_0 + \beta_1 \cdot \text{renda} + \beta_2 \cdot \text{gênero} + \beta_3 \cdot \text{educação} + \epsilon\]Onde $\beta_0, \beta_1, \beta_2, \beta_3$ são os coeficientes estimados e $\epsilon$ é o erro aleatório.
Para a renda, o modelo seria:
\[\text{renda} = \beta_0 + \beta_1 \cdot \text{idade} + \beta_2 \cdot \text{gênero} + \beta_3 \cdot \text{educação} + \epsilon\]O método pmm (Predictive Mean Matching) é especialmente útil porque gera valores que existem no dataset original, preserva a distribuição original das variáveis, e é robusto a outliers. Isso significa que você não vai acabar com valores impossíveis ou que distorcem completamente a distribuição dos seus dados.
Quando Usar MICE?
Nem todo problema de dados ausentes precisa do MICE. Se você tem apenas 2% de dados ausentes em uma única variável, usar a média pode ser perfeitamente aceitável. O MICE brilha quando você tem dados ausentes em múltiplas variáveis com padrões complexos de ausência.
Imagine um dataset de clientes onde idade, renda e gênero têm dados ausentes, mas não de forma aleatória. Pessoas com renda alta podem ser menos propensas a reportar idade. Pessoas mais velhas podem ter mais dificuldade para preencher formulários online. Nesse caso, o MICE é ideal porque ele consegue capturar essas correlações entre as variáveis.
Por outro lado, se você tem restrições computacionais severas ou se os dados ausentes são completamente aleatórios, métodos mais simples podem ser suficientes. O MICE também não é necessário quando você tem poucos dados ausentes (menos de 5%) e os padrões de ausência são muito simples.
A regra de ouro é: use MICE quando a complexidade dos dados ausentes justifica a complexidade da solução. Se você está construindo modelos que precisam ser robustos e confiáveis, o MICE vale o investimento. Se você está fazendo uma análise exploratória rápida, talvez a média seja suficiente.
A Armadilha da Imputação Simples
Muitos analistas ainda usam métodos simples como preenchimento com média ou moda, deleção de linhas com dados ausentes, ou imputação com valores constantes. Esses métodos podem parecer mais simples, mas eles subestimam a variabilidade dos dados, distorcem as correlações entre variáveis, produzem intervalos de confiança muito estreitos e podem introduzir viés na análise. O problema é que quando você preenche todos os valores ausentes com a média, você está assumindo que não há diversidade nos dados ausentes, o que raramente é verdade. Quando você deleta linhas com dados ausentes, você está perdendo informação valiosa e pode estar introduzindo viés de seleção. E quando você usa valores constantes, você está criando padrões artificiais que não existem na realidade.
O Impacto no Negócio
Imagine que você está construindo um modelo de churn. Com dados ausentes mal tratados, você pode perder clientes valiosos por não identificá-los corretamente, investir em estratégias erradas baseadas em dados distorcidos, e subestimar riscos por não considerar a incerteza. Com MICE, você tem modelos mais robustos que refletem a realidade dos dados, estimativas de incerteza que informam decisões, e análises mais confiáveis que resistem à validação. A diferença não é apenas técnica - é financeira. Um modelo que identifica corretamente 80% dos clientes que vão cancelar é muito mais valioso que um modelo que identifica apenas 60% porque não tratou adequadamente os dados ausentes.
Lições Aprendidas
Depois de anos trabalhando com dados ausentes, aprendi algumas lições que valem ouro. A primeira é que dados ausentes não são lixo - eles carregam informação valiosa sobre padrões de comportamento. Quando alguém não preenche sua idade em um formulário, isso pode dizer muito sobre sua relação com a tecnologia ou privacidade.
A segunda lição é que uma única imputação não captura a incerteza inerente aos dados ausentes. Sempre gere múltiplas versões dos dados. É como ter várias opiniões de especialistas em vez de confiar em apenas uma.
A terceira lição é validar suas imputações. Compare as distribuições antes e depois da imputação. Verifique se as correlações fazem sentido. Se a correlação entre idade e renda mudou drasticamente após a imputação, algo está errado.
Por fim, sempre documente o processo. Quais variáveis foram imputadas? Com quais métodos? Quantas iterações foram usadas? Seis meses depois, você vai agradecer por ter documentado tudo. A ciência de dados é um trabalho em equipe, e a documentação é o que permite que outros (ou você mesmo no futuro) entendam e reproduzam seu trabalho.
Conclusão
O MICE não é apenas uma técnica estatística. É uma filosofia sobre como lidar com a incerteza inerente aos dados reais. Em um mundo onde dados ausentes são a regra, não a exceção, dominar o MICE é essencial para qualquer cientista de dados que queira fazer análises confiáveis.
A próxima vez que você encontrar dados ausentes, não se contente com a média. Use o MICE. Seus modelos vão agradecer.
E seus clientes também.
Quer ver o MICE em ação? Confira como ele foi usado para tratar dados ausentes no case study sobre dados desbalanceados.
Comentários